The Mathematical Accuracies and Inaccuries of Infinite Jest

David Foster Wallace's magnum-opus Infinite Jest features a surprisingly high amount of mathematical inaccuracies for it being written by a man in love with math. But like the deliberate man Wallace was, much of his errors are explained by intention rather than recklessness.

While studying philosophy at Amherst College, Wallace concentrated in modal logic and mathematics. He describes in his essay “Derivative Sport in Tornado Alley” that topology and calculus was his language to understand the grid-lines and curvature of the horizon of the Midwest, and was a catharsis for his homesickness for Illinois.

But Wallace’s mathematical skills lack reliability. In 2003, Wallace published Everything and More: A Compact History of Infinity, which was panned by mathematicians. “Crippling errors abound,” said mathematician Rudy Rucker.

It’s no surprise that mathematics, both accurate and inaccurate, infiltrated Infinite Jest. Here are the seven most striking examples of math in Infinite Jest, explained.

1. Dr. Incandenza's Philosophy on Tennis and Wallace’s Obvious Contempt for Linear Dynamical Systems 

Were he now still among the living, Dr. Incandenza would now describe tennis in the paradoxical terms of what's now called 'Extra-Linear Dynamics.' And Schtitt, whose knowledge of formal math is probably about equivalent to that of a Taiwanese kindergartner, nevertheless seemed to know what Hopman and van der Meer and Bollettieri seemed not to know: that locating beauty and art and magic and improvement and keys to excellence and victory in the prolix flux of match play is not a fractal matter of reducing chaos to pattern. Seemed intuitively to sense that it was a matter not of reduction at all, but — perversely — of expansion, the aleatory flutter of uncontrolled, metastatic growth — each well-shot ball admitting of n possible responses, n2 possible responses to those responses, and on into what Incandenza would articulate to anyone who shared both his backgrounds as a Cantorian continuum of infinities of possible move and response, Cantorian and beautiful because infoliating, contained, this diagnate infinity of infinities of choice and execution, mathematically uncontrolled but humanly contained, bounded by the talent and imagination of self and opponent, bent in on itself by the containing boundaries of skill and imagination that brought one player finally down, that kept both from winning, that made it, finally, a game, these boundaries of self. (pg. 81)

In footnote 34 (pg. 994), Extra-Linear Dynamics is characterized as:

A.k.a., 'E.L.D.,' that still-green shoot off the pure branch of math that deals with systems and phenomena whose chaos is beyond even Mandelbrotian math's Strange Equations and Random Attractants, a delimiting reaction against the Chaos Theories of fractal-happy meteorologists and systems analysts, E.L.D., whose post-Gödelian theorems and nonexistence proofs amount to extremely lucid and elegant admissions of defeat in certain cases, hands thrown up w/ complete deductive justification. 

A less inflammatory name for E.L.D. is linear dynamical systems, a branch of chaos theory which uses linear equations to understand seemingly random processes which are highly sensitive to change. Benoit Mandelbrot was a 20th century mathematician who studied fractals and chaos theory, and who popularized the Mandelbrot Set

Wallace also strongly implies that mathematicians working in linear dynamical systems justify their failures by relying on Gödel’s Incompleteness Theorem as an excuse.

"Cantorian" is a reference to mathematician Georg Cantor. As described in footnote 35:

. . . the man who proved some infinities were bigger than other infinites, and whose 1905-ish Diagonal Proof demonstrated that there can be an infinity of things between any two things no matter how close together the two things are, which D. Proof deeply informed Dr. Incandenza's sense of the transstatistical aesthetics of serious tennis.

Wallace’s description of Cantor is less biting than his description of linear dynamical systems. Cantor did prove that some infinities are larger than others through his separation of infinity into two different concepts: transfinite numbers and absolute infinity. However, Cantor’s understanding of absolute infinity is in dispute.

This 1905-ish Diagonal Proof refers to Cantor’s diagonal argument, published in 1891, proves that the set of real numbers is uncountable, and that an infinite amount of real numbers exists between any two real numbers. The uncountability of real numbers may seem obvious because the set of real numbers is infinite, but it is not. The set of all rational numbers is countable, for example, yet still infinite.

Cantor’s continuum hypothesis states that there is no set of numbers which has a level of countability in between the complete countability in rational numbers and the complete uncountability of real numbers.

Dr. Incandenza’s appreciation of Cantor also makes sense, given that the diagonal argument is used in Gödel’s proof of the first Incompleteness Theorem. Gödel also proved in 1940 that the negation of the continuum hypothesis is impossible to prove in standard set theory.

2. The Allocation of Nuclear Warheads and the Mean-Value Theorem

Eschaton is a yearly game at the Enfield Tennis Academy, involving 400 tennis balls. Each ball represents a 5-megaton thermonuclear warhead.

Imagine Eschaton as a life-sized game of Risk, but instead players moving mini-soldiers across a board to represent troop movement, players launch decayed tennis balls across different courts to represent nuclear annihilation.

But Eschaton is no silly matter, and requires meticulous calculations to standardize the game each year. 

Practical distribution of total megatonnage requires a working knowledge of the Mean-Value Theorem for Integrals (pg. 323)

In footnote 123 (pg. 1023):

Pemulis here, dictating to Inc . . .

Say you’ve got a Combatant and a record of his past GNP/Military // Military/Nuke ratios. We want to give the Combatants the like exact average of all the past megatonnages he’s gotten in the past. The exact average is called the ‘Mean Value,’ which ought to give us a bit of a giggle, given the hostility of the context here. . .

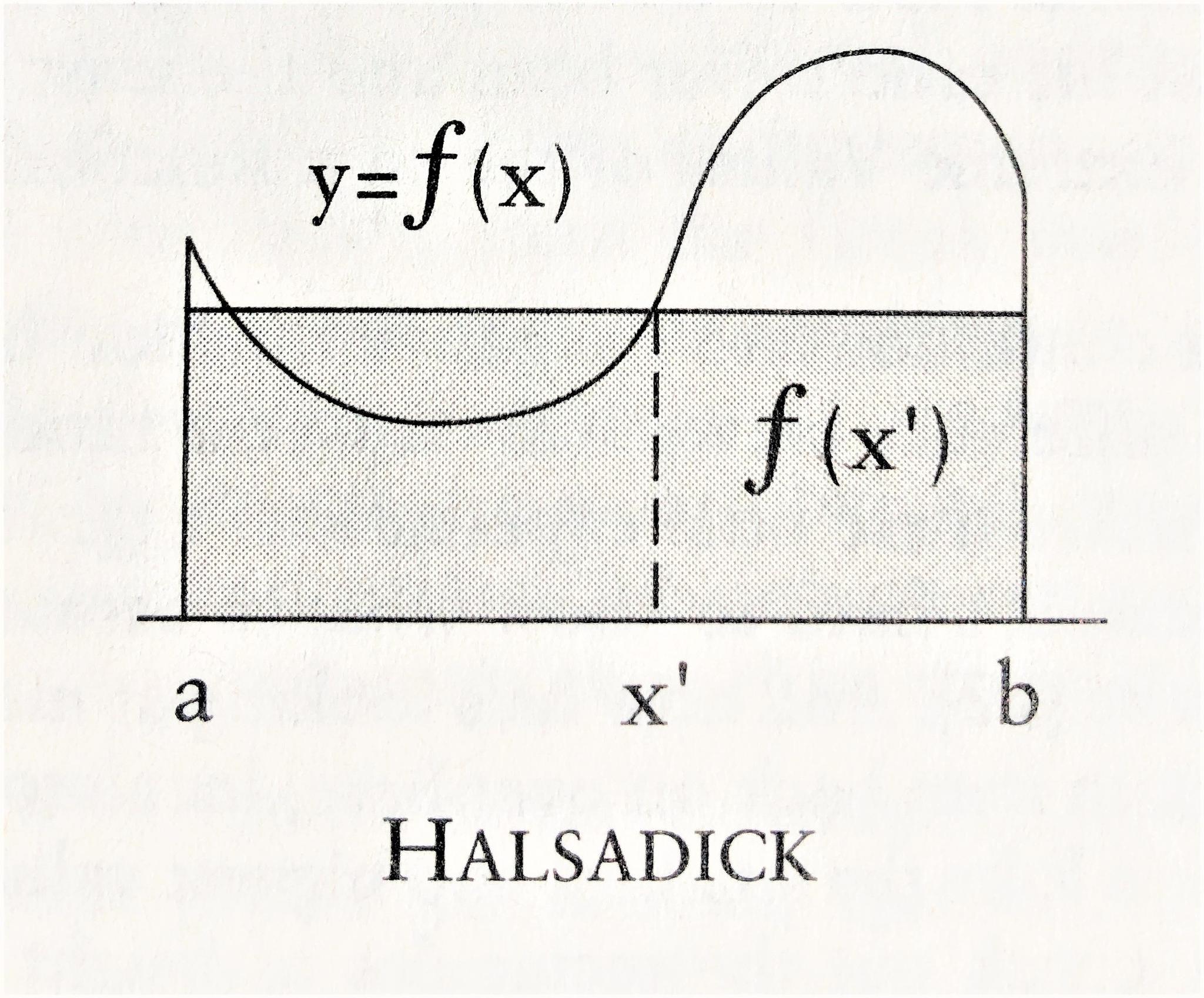
The Mean Value Theorem for integrals states that, for a function  f(x) that is continuous, the area under the curve f(x) from the interval x = a to x = b is the same as the area of a rectangle from a to b with a height of x’.
Pemulis’s use of the mean-value theorem to allocate nuclear tennis balls is clever, but misapplied. First, the mean value theorem is a theoretical tool for proving the existence of x' but provides no way to actually calculate the value of x’.

Second, the mean-value theorem would only be applicable to a continuous function, but not a dataset like the number of tennis balls. Pemulis could just as easily calculate the mean by adding all prior data in the set and dividing by the total number. No integrals involved.

Wallace knew these errors. Wallace wasn’t the biggest fan of calculus, but he had a deep love for mathematical rigor. Even if Wallace hadn’t noticed these errors, his editor would’ve. He also hired a mathematics graduate student at the University of Illinois to fact-check the equations and technical details.

Much of this footnote is through dialogue from Michael Pemulis, who Wallace once described as “one of the book’s Antichrists.” While Wallace wasn't wrong, Pemulis was. Pemulis is not as smart as he thinks he is.

You can find a more thorough analysis of the footnote and Pemulis’s arrogance on Collin Mckinney’s blog, the Oats Interactive.

3. Finding the Fire Blast Area of A Nuclear Warhead in Toronto
In the game Eschaton, the fire area from an air-blast (or, a tennis ball) is represented in as 2pi times bigger than the blast area. The total fire area for Toronto is represented by the equation

2π/(1/total Toronto area in m²)

For every additional m² of the Toronto region in Eschaton, the blast area expands by 2π. The circular expansion of fire does align with damage zone modeling from nuclear detonation done by the U.S. Department of Health and Human Services, but Pemulis’s equation fails to account for the compounding fire blast area that would happen if multiple tennis balls were launched at once. It is fair to assume that Pemulis had no knowledge of this modeling data.

And because Toronto has many sub-code skyscrapers, the fire area is optimized. This equation, of course, cannot be generalizable to other regions on the map of Eschaton.

4. The Probability of a 54-54 Result in a 108 Game Tournament

But so a normal meet between two junior teams is the best out of nine matches, whereas this mammoth annual early-November thing between E.T.A. and P.W.T.A. will try to be the best out of 108. A 54-match-all conclusion is extremely unlikely - odds being 1 in 2²⁷ - and has never happened in nine years (pg. 259)

This measurement is inaccurate by seven orders-of-magnitude.

The probability of 108 matches ending with exactly 54 wins for E.T.A.(Team A), and 54 wins for P.W.T.A.(Team B), can be calculated by the following:

(the number of outcomes resulting in a 54-54 tie)/(the number of all possible outcomes)

The denominator can be calculated simply by taking n, the number of possible outcomes in any given game (for a tennis match, there are 2 outcomes, assuming no chance of a tie), and raising n to the amount of matches m. 2¹⁰⁸

The numerator is a more complex combinatorial calculation. The numerator is the total number of ways in which Team A can achieve 54 victories (we’ll assign this the value p). in a 108 game tournament. For example, Team A could win the first 54 matches, and lose all subsequent matches, or win the first 53 matches and then lose the next 54, and win the last match, etc.

Or, by (m!/(m-p)! * p!)

The correct odds of a 54-54 conclusion at the 108-Game tournament between E.T.A. and P.W.T.A. is therefore (108!/(54! *54!))/(2¹⁰⁸), or 0.076, over seven orders-of magnitude off from Wallace’s original calculation of 0.00000000745.

Even factoring in the chance of any given match resulting in a tie results in a probability of 0.00000000000000000000745 - thirteen orders-of-magnitude off in the other direction.

This inaccuracy is perplexing, given that this error is not made in dialogue, but in narration. This error is additional evidence to the theory that Infinite Jest is not narrated by an omniscient narrator, but instead by a character within the story.

5. Door Knobs, Cycloids, and the Solution to the Brachistochrone Problem

The round knob and half its interior hex bold fell off and hit my room’s wooden floor with a loud noise and began then to roll around in a remarkable way, the sheared end of the hex bolt stationary and the round knob rolling on its circumference, circling it in a spherical orbit, describing two perfectly circular motions on two distinct axes, a non-Euclidian figure on a planar surface, i.e., a cycloid on a sphere:

The closest conventional analogue I could derive for this figure was a cycloid, L’Hopital’s solution to Bernoulli’s famous Brachistochrone Problem, the curve traced by a fixed point on the circumference of a circle rolling along a continuous plane.  But since here, on the bedroom’s floor, a circle was rolling around what was itself the circumference of a circle, the cycloid’s standard parametric equations were no longer apposite, those equations’ trigonometric expressions here becoming themselves first-order differential equations.(pg. 502)

Johann Bernoulli’s brachistochrone problem poses two points A and B on a vertical plane and asks the reader to find the shortest curve from A to B acted on only by gravity. The solution to this problem is a cycloid, the circular path traced by a single point on the circumference of a circle when it rolls in a straight line.

The solution to this problem was not just discovered by L’Hopital, but by Newton, Leibniz, and Bernoulli as well. Part of the proof for the solution involves the parametric equation X = (1/2)k²(θ - sin θ). Wallace is right; given the three-dimensionality of the lost doorknob, these equations become irreparably complex.

6. Not-So-Good Derivative Advice

'You use your goddamn imagination, Inc, plus a couple prescribed limits. Which they won't fuck with you on limits on the general test, trust me. This is a big pink titty compared to an Eschaton calculation. <strong>You move the two points you're doing Rise-over-Run on infitesimally close together, you end up with a plug-in formula.’

'Can I tell you about my dream now and then we'll use the momentum from that to plow through this?’

'Just write this on your wrist or something. <strong>Function x, exponent n, the derivative's going to be
nx + x^n-1 for any kind of first-order rate-of-increase thing they're going to ask you. </strong> This assumes a definable limit, of course, which no way they're going to fuck with you on limits on the fucking Boards.’(1063)</blockquote>

Given the intentional misspelling of “infinitesimally,” I’m certain that Pemulis’s error that the derivative of a function xⁿ is calculated as nx + x^n-1 instead of nx^n-1 is intentional on the part of Wallace.

7. Infinite Jest as a Fractal Itself

In a 1996 Interview with literary critic Michael Silverblatt, Wallace said that Infinite Jest itself was structural like a fractal, a never-ending geometrical pattern which is created by repeating a simple pattern, like an equation, through a feedback loop.

One example of a fractal is the Sierpinski Triangle, sometimes called the Sierpinski Gasket. The fractal is an equilateral triangle, which is initially subdivided into four smaller, equally-sized triangles. The center triangle is left blank, and then each remaining subdivision is divided again using the same process.

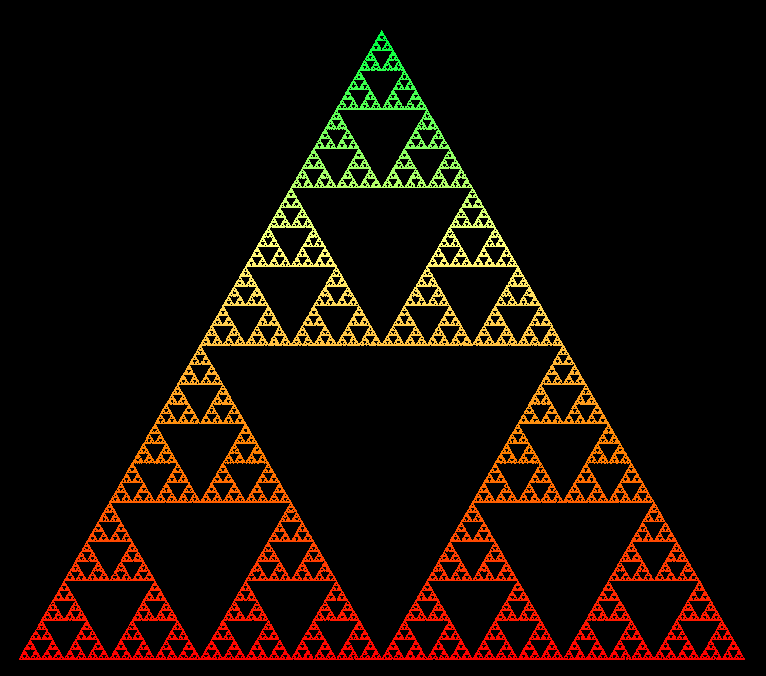
It's actually structured like something called a Sierpinski Gasket, which is a very primitive kind of pyramidical fractal, although what was structured as a Sierpinski Gasket was the first- was the draft that I delivered to [my editor] Michael in '94, and it went through some I think 'mercy cuts', so it's probably kind of a lopsided Sierpinski Gasket now.

Infinite Jest is split into three plotlines - E.T.A., the Ennett House Drug and Recovery House, and Quebecois Terrorism – just like the three resulting triangles in the first division of the Gasket (excluding the middle, blank triangle). Each plotline features a multitude of subplots that further divide into microcosmic vignettes. This structure is unforgiving, just like Infinite Jest’s timeline, narration, and dialogue, none of which offer any relief to the reader. The mathematics of Infinite Jest might just be the most straightforward part of the book - by far.